Relativity isn't Necessarily Relativistic
Thoughts on Space and Time Part 1: Einstein's Physics Isn't Necessarily All Bad

Space and Time - Part 1: Einstein's Physics Isn't Necessarily All Bad
This is the first (official) part of a larger series on space and time, the important, mysterious, and always paradoxically hidden aspects of our lives now—and perhaps in some altered way—within their paradoxical inversion in the pleroma of eternity. For now, this is just a brief prologue on Relativity and why it might be alright to use it, at least for now, to justify conclusions I will expand on later about both.
Relativity Isn’t Necessarily Bad
Einstein’s Relativity, both of the special and general form, is not necessarily a morally relativistic, deconstructionist, and modernist theory in the way that the physical sciences (and all the others) have been since Descartes and Hobbes.1 Some have used it that way, admittedly. The relativity of space and time is sometimes used to justify moral relativity, or full-on postmodernism. But this doesn’t have to be the case.
Rather, in the way that relativity relates space and time to each other, and beings to these and to each other, it returns us to an older set of ideas that preceded our “secular age”2 and reminds us of what it properly means to be a material being.
This is not to say that it is correct. Relativity has many issues, especially in its later general form (why can it get away with necessitating 95% of the universe being invisible and unknowable, is that science?). It’s also treated as so much of a golden calf by today’s sciences alongside the almost certain to be fraudulent string theory that I’m predisposed to have doubts for that reason alone. See any interview of Eric Weinstein on any topic for more about what theories might go “beyond” relativity. Others have raised concerns that the traditional story of Einstein and how he discovered his theories is baloney. I’m not sure about this either. The “physical evidence” so far “mostly” checks out, unless you are willing to accept the intriguing yet unpopular idea of a stationary earth and revolving universe, which interestingly does away with the need for postulating all of Einsteinian relativity’s claims about space and time even as it would produce the same measurable results. See Robert Sungenis of The Principle for more on this:
Again, I’m not sure. A counter-scientific revolution would be very very interesting to live through, especially so if it restored the Medieval (and Catholic) worldview so beautifully portrayed (and so wonderfully open to the transcendent) by C.S. Lewis in The Discarded Image to being an image no longer discarded.
However, if relativity is true, as most people who do have physics degrees (for whatever remaining time credentials have any meaning) currently claim, the Christian, or more broadly Thomist/Aristotelian should rejoice that Einstein replaced Newton.
Einstein’s relativity tells us if we stay perfectly stationary in space, we can never stop changing. We are always moving at velocity C, the speed of light, something we recognize by means of four vector momentum,3 through spacetime whether we like it or not. It just so happens that most of our motion usually occurs through time. You’re always moving to the future, right, and never staying in stasis, right? There are more mathematical ways to illustrate this, but few visible metaphors, so I may just leave that part at that. When one moves through space, however, in Einstein’s relativistic framework, one moves less through time, and the vector sum of the two “motions”, if time is considered as a fourth dimension and related mathematically to the other three, will always be a constant, the velocity C, the speed of light.4
This relationship, however meaningless it may sound if you can’t imagine it, leads to a better balance and contrast between the everlasting objects of philosophical discussion since the pre-Socractics, being and change, than the method the Newtonian (think Cartesian) physics that it replaced.
Isaac Newton’s physics is ideologically descended from Descartes’ dualism and prioritization of self and quantities above all things besides, of course, himself. Descartes thought a lot about himself. I guess that’s what the philosophical tradition he founded (I’ll just call it what it is, modernity) is all about in all things, as you can see the same outcome in Renaissance art as I wrote about last week. In the Newtonian frame space and time are absolute, making them seem almost as if they are beings themselves rather than their Aristotelian categorization as accidents of beings. Space and time are the stage, the background, yes, for the actions of Newtonian physics, but they are important in their absoluteness in such a way that they’re almost as seemingly important as the beings themselves. Substances pass through space and through time as if through beings, as if space and time are beings, and are the most important beings of the universe in fact. To Newton, the stage, because it is what is able to be mathematically analyzed, measured, and understood, is more important than the beings that are being appellated with such measurements.
The accidental characteristics of beings for Newton are more important than the beings themselves because it is the accidents that we are interested in and describe the quantities we care about within his framework of physics. To him, we couldn't care less whether a moving object we are describing is light, a bowling ball, or a fighter jet. All we need and care about are a few numbers and his equations. The objects don’t really matter all too much. Endless space and endless time are the real big kids on the block. Everything answers to time and space rather than time and space answering to substantial things or substances. With Newton, in the vein of Descartes’ skepticism, we lose sight of reality in the forgetfulness of real, solid, physical things as being beings themselves rather than sideshows.
Perhaps Einstein doesn’t bring us all the way back to an Aristotelian prioritization of substance and subjects prior to accidents in their role as the foundation for accidents. And he probably didn’t even intend to do so, as Paul Johnson notes in Modern Times when he describes the social effects of relativity during Einstein’s time, but relativity, if rightly understood, gives us at least a partial return to our Aristotelian heritage.
With Einstein, paradoxically, since time and space are more front and center in their constantly warping and changing, they actually fall back to a lower and more proper place. Substances, material beings, cannot stop undergoing change because they are constantly moving through time and possibly space and paradoxically must be considered as more real than the variously perceived and varying details, the accidents, which we are using to measure and understand them.
To be a material object, is, in the post relativity world, to always be in motion, either through space or through time. But the fact that we are always necessarily moving also makes us more aware that there must be something more static and unchanging underlying the continual change. Everything is always moving, which makes it more clear that we cannot have a static, unchanging universe but must come from somewhere and be headed towards somewhere, whether those somewheres be somewhere else in space, in time, or even, perhaps, outside of the bounds of change in the accidents in space and time entirely. In relativity, however, it becomes abundantly clear in the absence of absolute space and time and their being relative to the observer, that space and time are accidental characteristics of beings. Perhaps, I’d push even further and specifically call them accidents in Aristotle’s category of relation. They are “said of” beings and “present in” beings, but are not the beings themselves. The being escapes the grasp of mere quantification. It is something more and has to be there. We need more than mere accidents. Yes, accidents are important and are what we use to observe beings. But there must be something more under the hood. And relativity at least points us there.
And Einstein himself once put it this way, when forced to summarize the general theory of relativity in one sentence:
“Time and space and gravitation have no separate existence from matter.”5
Take out his admittedly still somewhat Cartesian and materialist “matter” and substitute “beings” and you’re back to Aristotle.
Personal Conclusions
In the end, mostly from my reading of Aristotle and Aquinas in general (Physics, De Anima, etc., and Aquinas’ commentaries therein) but influenced positively by Einstein I’ve come to the following definitional thoughts on space and time. These have been (partially) checked out by Thomist professors, but are still somewhat experimental. I share them because of the interesting conclusions in italics. (Interesting at least to me.)
Space and time are in the categories of place and time respectively. Each is a type of quantity, following from the fact that every material being must have proper dimensions and be subject to change.
Space and time, it is important to constantly remind oneself, are not substances. They have being as accidents of quantity only in relation to material beings as their subjects.
Now they are also proper accidents. Every material being must have them in some fashion.
For Aristotle, time is the measure of change and change is the measure of time. Time is not a substance, quantity, or quality, it fits into the category of relation, specifically between the states of potency and act for one being.
Space and time are both types of quantitative limitations on actuality for beings, space being the particular type of limitation on interaction between two beings, or between the parts of one being, time, on the other hand, is the limitation or gap between the states of potency and act and the measure of distinction between these two states.
This is an expansion on an idea used in a brief two-page assignment I wrote for a class at Wyoming Catholic College about three years ago. For more thoughts on relativity, here is what I wrote way back then to summarize the class: https://docs.google.com/document/d/1DGqURTUBf1ZRfG9rpfiwYMn3pn-MquJ-pT7sYnqJ-sw/edit?usp=sharing
Charles Taylor, A Secular Age.
From the document linked in footnote 1:
Four-vector momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime.
We’ve seen the interrelationship between space and time through relativity above. We’ve also been interested even from the time of classical physics in the conservation of momentum. However, from different reference frames, any object can seem to have a different momentum in the three ordinary dimensions of space. But if we relate to these momentum components to the perhaps seemingly different idea of energy, treating it as a vector-like quantity on the same level as the other momentum vector components we find that they transform together as a single invariant quantity even between differing inertial coordinate systems.
Energy and momentum transform together, such that they together produce a single total and invariant quantity that is “sliced” or perceived in different ways depending upon your inertial reference frame.
What this means, however, is that we can treat energy as the time component of four-momentum, which leads to the interesting conclusion that the energy (or mass) which an object possesses is merely the momentum the object has through time. In other words, objects are always moving, they always possess momentum of some type. Exactly how much of this momentum is through space in the ordinary sense of momentum and how much of it is through time varies depending on your frame of reference.
In some perspectives an object will seem to have more momentum through space, that is, it will be perceived as moving faster but will be seen as experiencing correspondingly less momentum through time (its proper time will be slowed down by the Lorentz factor). In other perspectives, it will seem to have more momentum through time but less through space.
The equations for transforming from the observed quantities of each momentum vector component in one coordinate system to those in another are as follows:
The spacetime interval is a sort of “distance” between two events that combines aspects of space distance and time interval. It is calculated by taking the distance in space between the two events (using the distance formulas we’ve derived from the Pythagorean theorem) and then subtracting the square of the time times the square of the speed of light.
Thus, we have a quantity invariant across transformations between coordinate systems
The resulting quantity s2 (or the square root of it, s, which is also sometimes called the interval, is invariant, meaning any reference frame will return the same resulting quantity. Differing reference frames will return differing differences in space or intervals in time between the two events, but the resulting quantity will be the same for any two events regardless of your coordinate system/ reference frame.
Another way of writing this invariance where our t units are chosen carefully to be in the same units as our space units (e.g. a space unit of ~186,000 miles or one light second and a time unit of one second, etc.)
https://www.spaceandmotion.com/Physics-Albert-Einstein-Theory-Relativity.htm





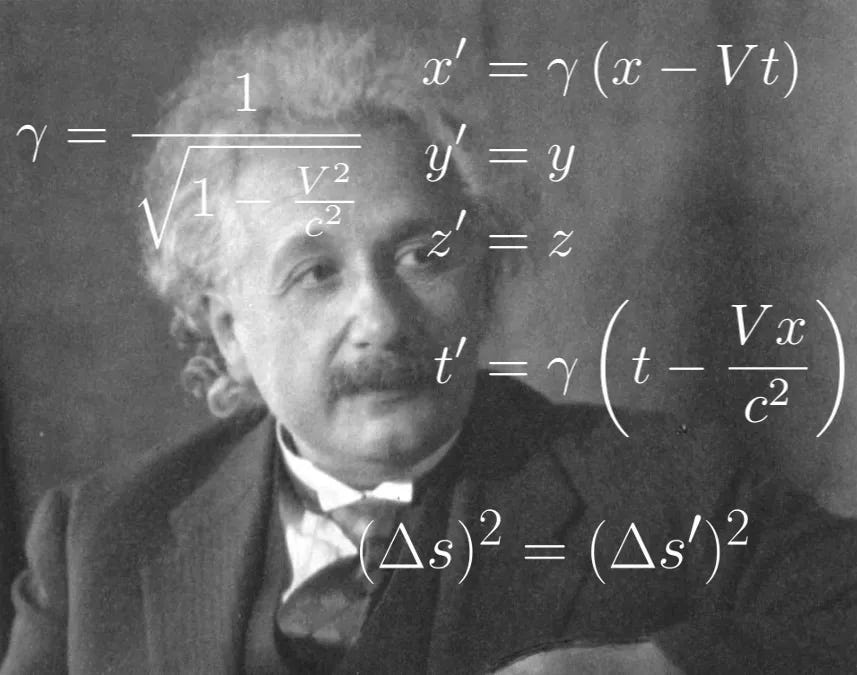

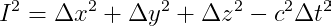

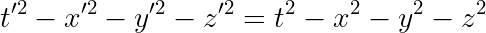
Mr Green, I believe you would be an excellent astrophysicist!